The motion of the particle is described by
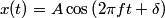 So, the particle's velocity is 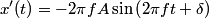 When x(t) = A/2 , 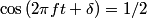 , so , so 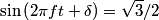 or or 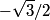 . So, the particle's speed is . So, the particle's speed is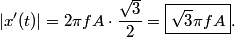 Hence, answer (B) is correct. |
The motion of the particle is described by
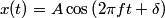 So, the particle's velocity is 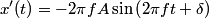 When x(t) = A/2 , 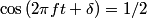 , so , so 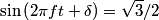 or or 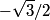 . So, the particle's speed is . So, the particle's speed is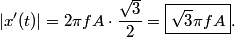 Hence, answer (B) is correct. |